ここからちょっと数学的な話になるので、結果(Matlabのコマンド)だけ知りたい方は下の方にスクロールして飛ばしてください。
さて、3次元(x,y,z)座標上のN×M個の3次元データ群P(xi,yj,zi,j)の最小二乗平面をSとし、次式のように定義できる
ここで、l,m,nは平面Sに対する法線ベクトルの要素である。zの値はx-y軸の座標xi、yjによって一意に決まるので、
これらの式を整理すると、
となる。この連立方程式の解は逆行列を用いて、次式のようになる。
となる。
さて、このような数式の通りにMatlabのプログラムを組んでいけばよい。実際に、Matlabで作成した例を下図fig.1(a)及び(b)に示す。fig.1(a)より、得られた最小二乗平面は、任意に与えた均一平面データを忠実に再現しており、正しく得られていることが分かる。また、fig.2(b)はある実測した平面の近似が得られていることが分かる。
clear
%%%%%%%%%%%%%%%%%%%%%%%%%%%読み込み%%%%%%%%%
test=csvread('test2.csv');
subplot(3,1,1)
surf(test);shading flat
colorbar
%%%%%%%%%%%%%%%%%%%%%%%%%%%%最小二乗法%%%%%%%%%%%
xnum=size(test,1);
ynum=size(test,2);
x(1:xnum)=1:xnum;
y(1:ynum)=1:ynum;
z(1:xnum,1:ynum)=test;
for i=1:xnum
for j=1:ynum
xz(i,j)=x(i)*z(i,j);
yz(i,j)=y(j)*z(i,j);
xy(i,j)=x(i)*y(j);
end
end
Sxz=sum(sum(xz));
Syz=sum(sum(yz));
Sz=sum(sum(z));
Sxy=sum(sum(xy));
Sx=j*sum(x);
Sy=i*sum(y);
Sx2=j*sum(x.^2);
Sy2=i*sum(y.^2);
A=[Sx2 Sxy Sx; Sxy Sy2 Sy; Sx Sy xnum*ynum];
Z=[Sxz; Syz; Sz];
W=A\Z;
w1=W(1);
w2=W(2);
w3=W(3);
l=-w1/(w1^2+w2^2+1)^0.5;
m=-w2/(w1^2+w2^2+1)^0.5;
n=1/(w1^2+w2^2+1)^0.5;
p=w3/(w1^2+w2^2+1)^0.5;
%%%%%%%%%%%%%%%%求めた平面の生成と表示%%%%%%%%%
for i=1:xnum
for j=1:ynum
z_2(i,j)=(-l/n)*x(i)+(-m/n)*y(j)+(p/n);
end
end
averagev=sum(sum(z_2))/(xnum*ynum);
subplot(3,1,2);
surf(z_2);shading interp;colorbar
subplot(3,1,3)
sa=abs(z-z_2);
surf(sa);shading flat;colorbar







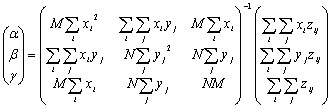


0 件のコメント:
コメントを投稿