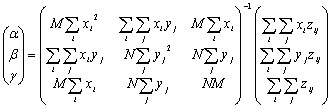いままで、数年間ここに近況などを書き込んでいましたが、
最近、研究者の情報はresearchmapに集約されていく流れですので、
今後はそちらへ移行いたします。
今までの記事はMatlabによる近似平面を作る記事以外はすべて非表示になりました。
近況などは、researchmapをご参照ください。
2018年12月5日水曜日
2013年2月20日水曜日
Matlabで平面の近似（最小二乗法）を計算する
実験で物体の平面計測をやっていると、測定値の平面分布に最も近似している平面を割り出す必要が生まれてくる。今回は、そういう要望に対してMatlabで行った計算について書きます。ネットや教科書には１元変数の曲線についての最小二乗法は、高次の場合も含めて沢山説明されているが、3次元平面の最小二乗法はなかなかないので、ここにまとめるのも少しは意義があることだと思います。
ここからちょっと数学的な話になるので、結果（Matlabのコマンド）だけ知りたい方は下の方にスクロールして飛ばしてください。
さて、3次元（x,y,z）座標上のN×M個の3次元データ群P(xi,yj,zi,j)の最小二乗平面をSとし、次式のように定義できる
（１）
（２）
と書きかえることができる。3次元データPのxi,yjでのｚの測定値をzijとすると、最小二乗平面Ｓとの差の二乗和Eijは、
（３）
となる。Ｅijが最小になる係数a,b,gを求めることで近似平面が求まる。そのためには、(3)式をそれぞれの係数で偏微分した値が0となる条件を求めればよい。従って、次式に示す連立方程式が生成される。
（４）
（５）
（６）
fig.1 計算結果
Matlabのプログラムは以下のようになる。（使用の際は、状況に応じて変数や読み込み方法等を変える必要があります。また、for文を行列の代入に変えることで動作が速くなる可能性があります）
clear
%%%%%%%%%%%%%%%%%%%%%%%%%%%読み込み%%%%%%%%%
test=csvread('test2.csv');
subplot(3,1,1)
surf(test);shading flat
colorbar
%%%%%%%%%%%%%%%%%%%%%%%%%%%%最小二乗法%%%%%%%%%%%
xnum=size(test,1);
ynum=size(test,2);
x(1:xnum)=1:xnum;
y(1:ynum)=1:ynum;
z(1:xnum,1:ynum)=test;
for i=1:xnum
for j=1:ynum
xz(i,j)=x(i)*z(i,j);
yz(i,j)=y(j)*z(i,j);
xy(i,j)=x(i)*y(j);
end
end
Sxz=sum(sum(xz));
Syz=sum(sum(yz));
Sz=sum(sum(z));
Sxy=sum(sum(xy));
Sx=j*sum(x);
Sy=i*sum(y);
Sx2=j*sum(x.^2);
Sy2=i*sum(y.^2);
A=[Sx2 Sxy Sx; Sxy Sy2 Sy; Sx Sy xnum*ynum];
Z=[Sxz; Syz; Sz];
W=A\Z;
w1=W(1);
w2=W(2);
w3=W(3);
l=-w1/(w1^2+w2^2+1)^0.5;
m=-w2/(w1^2+w2^2+1)^0.5;
n=1/(w1^2+w2^2+1)^0.5;
p=w3/(w1^2+w2^2+1)^0.5;
%%%%%%%%%%%%%%%%求めた平面の生成と表示%%%%%%%%%
for i=1:xnum
for j=1:ynum
z_2(i,j)=(-l/n)*x(i)+(-m/n)*y(j)+(p/n);
end
end
averagev=sum(sum(z_2))/(xnum*ynum);
subplot(3,1,2);
surf(z_2);shading interp;colorbar
subplot(3,1,3)
sa=abs(z-z_2);
surf(sa);shading flat;colorbar
ここからちょっと数学的な話になるので、結果（Matlabのコマンド）だけ知りたい方は下の方にスクロールして飛ばしてください。
さて、3次元（x,y,z）座標上のN×M個の3次元データ群P(xi,yj,zi,j)の最小二乗平面をSとし、次式のように定義できる
（１）
ここで、l,m,nは平面Sに対する法線ベクトルの要素である。zの値はｘ-ｙ軸の座標xi、yjによって一意に決まるので、
（２） （３） （４）
これらの式を整理すると、
（５）
となる。この連立方程式の解は逆行列を用いて、次式のようになる。
（６）
この計算はMatlabのコマンドで簡便に行うことができる。（逆行列の求め方は長くなるので、割愛させていただきます。）また、得られたa,b,gからl,m,n,pは、
（７）
（７）
となる。
さて、このような数式の通りにMatlabのプログラムを組んでいけばよい。実際に、Matlabで作成した例を下図fig.１(a)及び(b)に示す。fig.1(a)より、得られた最小二乗平面は、任意に与えた均一平面データを忠実に再現しており、正しく得られていることが分かる。また、fig.2(b)はある実測した平面の近似が得られていることが分かる。
fig.1 計算結果clear
%%%%%%%%%%%%%%%%%%%%%%%%%%%読み込み%%%%%%%%%
test=csvread('test2.csv');
subplot(3,1,1)
surf(test);shading flat
colorbar
%%%%%%%%%%%%%%%%%%%%%%%%%%%%最小二乗法%%%%%%%%%%%
xnum=size(test,1);
ynum=size(test,2);
x(1:xnum)=1:xnum;
y(1:ynum)=1:ynum;
z(1:xnum,1:ynum)=test;
for i=1:xnum
for j=1:ynum
xz(i,j)=x(i)*z(i,j);
yz(i,j)=y(j)*z(i,j);
xy(i,j)=x(i)*y(j);
end
end
Sxz=sum(sum(xz));
Syz=sum(sum(yz));
Sz=sum(sum(z));
Sxy=sum(sum(xy));
Sx=j*sum(x);
Sy=i*sum(y);
Sx2=j*sum(x.^2);
Sy2=i*sum(y.^2);
A=[Sx2 Sxy Sx; Sxy Sy2 Sy; Sx Sy xnum*ynum];
Z=[Sxz; Syz; Sz];
W=A\Z;
w1=W(1);
w2=W(2);
w3=W(3);
l=-w1/(w1^2+w2^2+1)^0.5;
m=-w2/(w1^2+w2^2+1)^0.5;
n=1/(w1^2+w2^2+1)^0.5;
p=w3/(w1^2+w2^2+1)^0.5;
%%%%%%%%%%%%%%%%求めた平面の生成と表示%%%%%%%%%
for i=1:xnum
for j=1:ynum
z_2(i,j)=(-l/n)*x(i)+(-m/n)*y(j)+(p/n);
end
end
averagev=sum(sum(z_2))/(xnum*ynum);
subplot(3,1,2);
surf(z_2);shading interp;colorbar
subplot(3,1,3)
sa=abs(z-z_2);
surf(sa);shading flat;colorbar
登録:
投稿 (Atom)